¶ 几种重要度因子(Importance Factor)的定义
下列项目的叙述中,表示可靠度,表示失效概率。
¶ 边缘重要性因数(MIF, Marginal Importance Factor)
The Marginal Importance Factor(MIF), introduced by Birnbaum, is defined as a measure of the variation of the system reliability according to the reliability of a component. The marginal important factor of the component can be written as:
The above equation evaluates how fast the system reliability increases according to the increase of the component reliability. So, to increase the system reliability, the reliability of the component having the largest MIF should be increased.
MIF定义为系统可靠性对某组件的可靠性的变化率,计算方程如上。换言之,某个组件的MIF等于其失效所带来的系统失效概率增量。
使用MIF指标指导可靠性设计的思路是:如果要改进某系统的可靠性,首先改进具有最大MIF的组件的可靠性。
¶ 紧急重要性因数(CIF, Critical Importance Factor)
与边缘重要性因数(MIF)类似,但是考虑了组件自身可靠性的影响,其计算方式如下:
其中为组件的失效概率,为系统失效概率。相对于MIF,CIF考虑到了提升可靠度的难度——如果某组件的失效概率已经很低了,则进一步提升其可靠度可能成本较高,因此应该适当降低其优先级。
¶ 判断重要性因数(DIF, Diagnostic Importance Factor)
组件的DIF指标评估组件的失效概率对于系统失效概率的贡献。
有时称为Fussel-Vesely.
¶ 风险增加价值(RAW, Risk Achievement Worth)
组件的RAW指标评估组件失效后系统失效率的相对增量,其计算公式为:
那些一旦失效就会引起系统失效的组件,其对应的RAW指标可能远远大于1.
有研究认为,该指标表征了不降低/维持组件的现有可靠性的重要程度。
有些文献中称为Risk Increase Factor.
¶ 风险降低价值(RRW, Risk Reduction Worth)
与风险增加价值(RAW)类似,该指标表征了当前组件永不失效()为系统带来的可靠性增量,其计算公式为:
¶ 两个简单算例与相应的计算报告
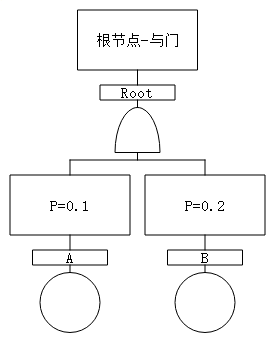
¶ 简单与门算例
故障树:

系统失效概率:
重要度因子:
| ID | 概率 | MIF | CIF | DIF | RAW | RRW |
|---|---|---|---|---|---|---|
| B | 0.20 | 0.90 | 0.6428571428571429 | 0.71428571428571441 | 3.5714285714285716 | 2.80 |
| A | 0.10 | 0.80 | 0.28571428571428575 | 0.35714285714285721 | 3.5714285714285716 | 1.4 |
¶ 简单或门算例
故障树:
系统失效概率:
重要度因子:
| ID | 概率 | MIF | CIF | DIF | RAW | RRW |
|---|---|---|---|---|---|---|
| B | 0.20 | 0.10 | 1 | 1 | 5 | 0 |
| A | 0.10 | 0.20 | 1 | 1 | 10 | 0 |
上表中RRW为零的原因是分母无穷大