¶ 直接实验法
最为简单直接的获取组件可靠度的方法,直接进行大批量可靠性实验来获取组件的可靠度。同时,在实验次数足够多的情况下,这也是精度最高的方法。
对于制造成本、实验成本不高的组件,如点火头,这是最为合适的方法。但对于固体火箭发动机中的多数组件,这一方法并不合适,原因包括:
- 单次实验成本过高,如装药点火实验成本较高,不适合大批次进行;
- 常出现无失效数据,即整个实验过程中没有任何样件发生失效,此时没有可以直接用于评估失效概率的数据,但显然不能据此认为目标组件可靠度为1;
- 组件耦合较为严重,例如对壳体的热实验一般必须使用真实装药,但该环境下的壳体爆破并不一定由壳体强度不足引发,还可能由装药裂纹引发。
由于这些原因的存在,尽管直接实验法在电子等行业得到了广泛应用,其在固体火箭发动机领域的出现频率并不高。
¶ 类比法
固体火箭发动机的一个突出特点是标准件少,大量使用定制零件,因此难以像电子与民用机械行业一样,直接利用原有的零部件的可靠性数据进行系统可靠性评估。但是,考虑到不同型号固体火箭发动机部件的相似性,在缺乏直接数据时可以使用类比法,在旧有发动机数据的基础上估计新发动机组件的可靠性。
从数学角度看,类比法本质上是插值法,通过在新、旧零件之间寻找相似性与变量来估计新零件的可靠度。可资利用的相似项目包括:
- 材质与工艺
- 结构与形状
- 尺寸
- 工作时间
- 工作负载
- 工作环境
类比法不能单独工作,必须在已有相关数据的情况下,才能使用类比法基于适当的数据进行类比和插值。
¶ 强度-应力分布法
强度-应力失效模式可以应用于固体火箭发动机中相当一部分组件,包括壳体、法兰失效、药柱裂纹甚至堵盖破裂压强,其特征是工作负载超出某一数值后失效立即发生,无时间积累性。
在无法进行大批量实验的情况下,遵循这一失效模式的组件的失效概率可以通过应力分布与强度分布算得,而压力、强度的分布模式与分布参数则可以通过低成本实验获取。
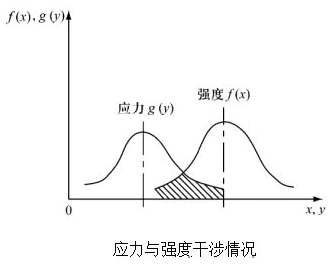
基于压力强度概率分布的失效概率计算方式如上图所示,图中阴影区域的积分面积即为失效概率。
在个别情况下,压力或强度的分布可能不是正态分布,但这不影响上述计算的适用性;只要能够提供具体的概率密度函数,上述计算就可以正常进行。
¶ 随机有限元法
有限元法可以精确地求解各类复杂结构实际行为,但是确定的有限元方法不能考虑变量的随机性,这样限制了有限元方法在可靠性分析中的应用。为了兼得两种方法的长处,产生了随机有限元(SFEM)或称概率有限元(PFEM)的思想,基于随机有限元的可靠性分析可以尽可能真实地评价简单或复杂系统的可靠性。它类似于确定性的有限元分析,但在分析中考虑了变量的不确定性。
简单来说,该方法类似于执行在每个网格上的应力-强度失效模型。在实际操作中,已经有了一系列算法保证该过程高效、精确地进行。
¶ 无失效数据分析法
这是一套在高可靠性产品的实际特点之上发展出来的计算方法,在一定程度上解决了在无任何产品失效的情况下估算产品可靠度的问题。
航天产品往往具有可靠性极高、批次小的特点,这经常造成其在整个可靠性实验中不出现任何失效现象。为了合理推算这种情况下产品的可靠性,目前已经发展出了一些基于贝叶斯理论的算法,通过添加合理的假设,估算组件的可靠度的下限。
现有理论主要针对寿命型产品发展而来,但通过适当的发展,这一理论与小子样相关理论结合,用于固体火箭发动机相关零件可靠度的估算。