¶ 问题概述
¶ LSM
固体火箭发动机的内弹道,指的是发动机工作时的压强-时间曲线。对其进行计算的基础,是要知道该发动机固体装药的燃面-肉厚曲线。
对于复杂装药,燃面-肉厚曲线一般需要通过计算机图形学方法来获取。各种图形学方法中,Level Set Method (LSM)是比较稳定的一种,能够正确处理燃烧过程中随平行层推移出现的拓扑变化。
然而,LSM需要耗费极大的计算资源,即使使用了GPU计算技术,以高分辨率网格进行仿真仍然需要几个小时。这不仅影响发动的设计进度,也让大规模的结构优化变得不甚可行。
¶ CNN
考虑到发动机装药的几何表示实际上可以看作是一个图形,“按平行层燃烧定理推移一步”这个行为,也可以看作是从一张图预测另一张图。而卷积神经网络CNN在这类问题中往往可以有较高的性能。使用CNN来解这个问题,是值得尝试的。应用神经网络的优点,主要有两条:
- 速度更快。神经网络的执行时间是常数,不需要迭代求解,且可以利用现有的大量优化到极致的计算软件甚至专用硬件。LSM方程需要迭代求解,程序需要自行编写。
- 稳定性好。解LSM方程需要注意CFL条件,对时间步长有限制。训练好的神经网络基本上不存发散问题,其等效CFL数可以大于1。
¶ 训练数据
在一般神经网络训练任务中,训练数据由人类提前标注。然而,对于用于解方程的神经网络,其训练数据可以通过解方程来获取。不但速度大幅加快,数据量也几乎没有限制。
具体方法是,先使用随机数生成器,产生大量的初始条件和边界条件,再在此基础上按正常方法进行LSM求解,将产生的每一步中间数据都存入数据库。下面两图分别是初始几何体的有向距离场与定义的速度场:


生成训练数据的流程:

¶ 网络结构
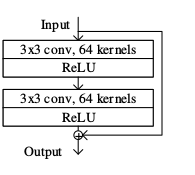
与普通的图片分类任务不同,这里是要在每一个像素上模拟方程求解,所以需要较多关于输入的精确信息。故网络结构选择了残差神经网络 ResNet.这种网络是卷积神经网络的一种,其特点在于,每隔几层,会有一条“捷径”,将离原始输入很近的信息引入进来。这样一来,虽然网络有很多层,但实际上网络不是太深。
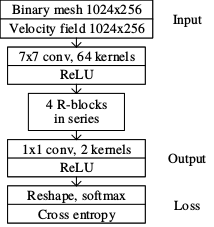
¶ 损失函数
损失函数的定义,是这个问题的难点。
直观来看,解方程问题的损失函数很容易定义:直接定义为网络输出与方程输出的差值的平方。然而,经过试验,这种做法效果相当差。
原因在于,LSM的输入和输出都是有向距离场。在高分辨率情形下,要求的数值精度极高。
Take our problem as example, we have placed 256 grids in range, which means the maximum possible difference between values of on two neighbouring nodes is . CFL condition limit propagation amount under . Suppose CFL factor is 0.8, the amount of change after one time step would be . To approximate equation solving, the difference between equation output and network output shall be at most . The required error bound is close to the precision limit of ordinary 32-bit float variable (). If we take reinitialization into account, required error bound would be even more stringent. Neural network is essentially an approximation method, training a network having such accuracy is extremely difficult.
经测试,按这种损失函数训练出来的神经网络,其产生的误差总和比前后两帧图像之差的总和还要要高,概括来说就是完全没法用。
回到起点,分析问题可以发现,这种现象的根本原因是:用有向距离场表达几何体所需的精度太高。换个思路,可以放弃有向距离场,改用最简单的笛卡尔网格来表达:将物体所在的空间划分为矩形网格,对于每个网格点,只关心其是/否处在目标几何体的范围内。
这样一来,原本要求高精度的拟合问题,被转换成了对每个网格点进行分类的问题。分类问题是神经网络最为擅长的领域,允许的误差限极大——以0.5为界,[0,0.5)定义为False,(0.5, 1]定义为True.
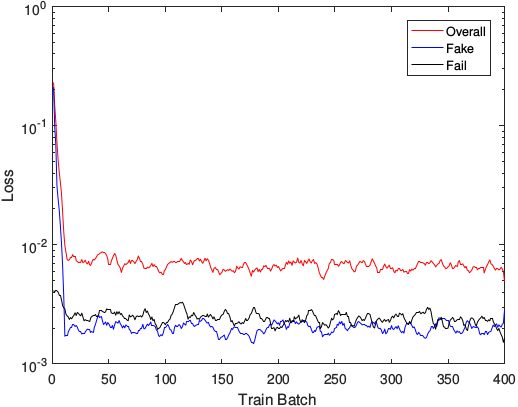
用改进过的损失函数,网络的训练很顺利:
训练:
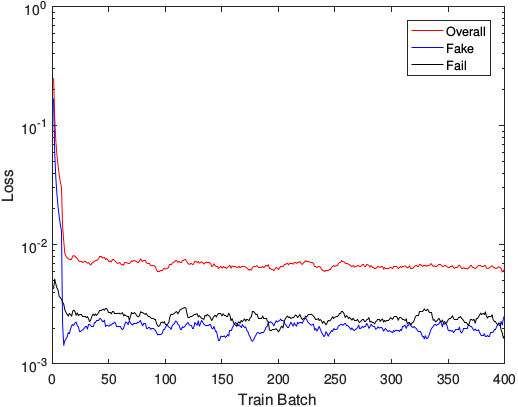
测试:
¶ 测试结果
将训练过的网络参数保存下来,重新随机生成一些几何体和速度场,令其预测下一步时的几何体形状,结果如图(红色像素为错误的点):

错误仍然存在,但区域不大,可以看出主要出现在几何体的边界区域。原因后面猜测。
将神经网络的输出再作为输入,迭代求解,并将每一步中神经网络的输出与一直采取正规LSM解法的结果进行对比,其误差曲线如下图:
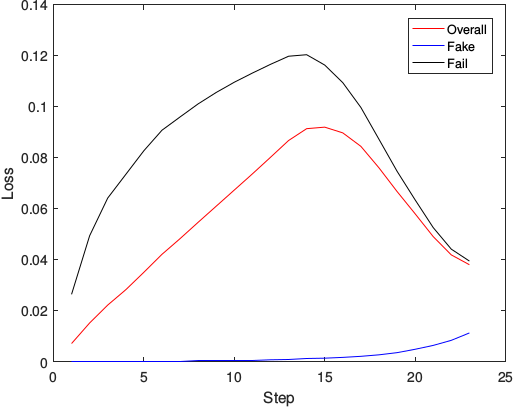
可以看出,误差有积累,但没有无限制地发散下去。可以认为该思路是可行的。
出现在边界上的误差,猜测是由于使用的卷积核过小。训练中所使用的等效CFL数为8,在一步当中,几何体边界最多前进了8格。然而,网络中用到的卷积核最大为7 x 7,后面的则全是3 x 3.网络中为了避免分辨率降低,网络中没有使用下采样层,故网络难以学习到8格之外的信息(7 x 7卷积核的半径仅为3).这一点应在后面的研究中修正。
Solving Level Set Evolving Using Fully Convolution Network
条目类型 会议论文
作者 Ran Wei
作者 Futing Bao
作者 Yang Liu
作者 Weihua Hui
日期 8/2017
语言 en
网址 http://ieeexplore.ieee.org/document/8047620/
访问时间 2018/12/2 21:15:43
版权 All rights reserved
地点 Hangzhou
出版社 IEEE
ISBN 978-1-5386-3021-1 978-1-5386-3022-8
页码 234-238
会议论文集标题 2017 9th International Conference on Intelligent
Human-Machine Systems and Cybernetics (IHMSC)
会议名称 2017 9th International Conference on Intelligent
Human-Machine Systems and Cybernetics (IHMSC)
DOI 10.1109/IHMSC.2017.61 <http://doi.org/10.1109/IHMSC.2017.61>