《Level Set Methods and Dynamic Implicit Surfaces》
Level Set的核心思想是用数量场中的等值面表示几何曲面,求解 Level Set 的实质,还是是用数值方法求解一个微分方程。既然涉及到空间微分方程,绕不开的一个问题就是数值微分。最简单的中心差分由于数值震荡的原因无法使用,迎风格式很简单很有效然而精度不高。Level Set 计算中最常用的 WENO 差分格式,然而这格式实在比较复杂,加之网上找到的资料多为流体方程求解所用,花了不少力气才看懂。
ϕ t + V ⃗ ∇ ϕ = 0 ϕ t + V ∇ ϕ = 0
其中
V ⃗ = { u , v , w } V = { u , v , w }
在一维情况下展开为:
ϕ n + 1 − ϕ n Δ t + u n ϕ x n = 0 Δ t ϕ n + 1 − ϕ n + u n ϕ x n = 0
可见,求解方程首先需要计算$${{\phi}^n_x}$$,即第n时间步上$${{\phi}x}$$的数值。 {i}} = {{\phi}_{x_i}}$$
CFL条件用于控制空间步长与时间步长,保持数值稳定性。一般认为,满足下式时,数值求解是稳定的,误差不会扩大:
Δ t < Δ x m a x { ∣ u ∣ } Δ t < m a x { ∣ u ∣ } Δ x
令α = Δ t m a x { ∣ u ∣ } Δ x α = Δ t Δ x m a x { ∣ u ∣ }
定义:
D + ϕ = ϕ + = ϕ i + 1 − ϕ i Δ x D + ϕ = ϕ + = Δ x ϕ i + 1 − ϕ i
D − ϕ = ϕ − = ϕ i − ϕ i − 1 Δ x D − ϕ = ϕ − = Δ x ϕ i − ϕ i − 1
迎风格式的思想是与物理实际相结合,运动方向是哪边来的,就利用哪边的导数信息(或者主要利用哪边的),故有:
ϕ i = { ϕ i − u i > 0 ϕ i + u i < 0 ϕ i = { ϕ i − ϕ i + u i > 0 u i < 0
至此,一切都很简单。
Hamilton Jacobi ENO格式,精度比上述迎风格式高,可以到三阶精度。ENO全称Essentially Nonoscillatiry,精选非震荡,听着有点像广告……u u ϕ + ϕ + ϕ − ϕ −
D i 0 ϕ = ϕ i D i 0 ϕ = ϕ i
2.一阶,定义在网格中间:
D i + 1 / 2 1 ϕ = D i + 1 0 ϕ − D i 0 ϕ Δ x D i + 1 / 2 1 ϕ = Δ x D i + 1 0 ϕ − D i 0 ϕ
3.二阶,定义在网格点上:
D i 2 ϕ = D i + 1 / 2 1 ϕ − D i − 1 / 2 1 ϕ 2 Δ x D i 2 ϕ = 2 Δ x D i + 1 / 2 1 ϕ − D i − 1 / 2 1 ϕ
4.三阶,定义在网格点上:
D i + 1 / 2 3 ϕ = D i + 1 2 ϕ − D i 1 ϕ 3 Δ x D i + 1 / 2 3 ϕ = 3 Δ x D i + 1 2 ϕ − D i 1 ϕ
##差分格式ϕ ( x ) ϕ ( x )
ϕ ( x ) = Q 0 ( x ) + Q 1 ( x ) + Q 2 ( x ) + Q 3 ( x ) ϕ ( x ) = Q 0 ( x ) + Q 1 ( x ) + Q 2 ( x ) + Q 3 ( x )
在x i x i
ϕ ′ ( x i ) = Q 1 ′ ( x ) + Q 2 ′ ( x ) + Q 3 ′ ( x ) ϕ ′ ( x i ) = Q 1 ′ ( x ) + Q 2 ′ ( x ) + Q 3 ′ ( x )
首先求一阶导数的估计,由于是 ϕ x − ϕ x − k = i − 1 k = i − 1
Q 1 ( x ) = ( D k + 1 / 2 1 ) ( x − x i ) Q 1 ( x ) = ( D k + 1 / 2 1 ) ( x − x i )
Q 1 ′ ( x ) = D k + 1 / 2 1 Q 1 ′ ( x ) = D k + 1 / 2 1
下面看Q 2 Q 2
Q 2 ( x ) = c ( x − x k ) ( x − x k + 1 ) Q 2 ( x ) = c ( x − x k ) ( x − x k + 1 )
两边求导:
Q 2 ′ ( x ) = c [ 2 ( i − k ) − 1 ] Δ x Q 2 ′ ( x ) = c [ 2 ( i − k ) − 1 ] Δ x
其中,c c
c = { D k 2 ϕ ∣ D k 2 ϕ ∣ < ∣ D k + 1 2 ϕ ∣ D k + 1 2 ϕ ∣ D k 2 ϕ ∣ > ∣ D k + 1 2 ϕ ∣ c = { D k 2 ϕ D k + 1 2 ϕ ∣ D k 2 ϕ ∣ < ∣ D k + 1 2 ϕ ∣ ∣ D k 2 ϕ ∣ > ∣ D k + 1 2 ϕ ∣
可以看出来,上面所谓“从k = i − 1 k = i − 1 Q 2 Q 2 k ∗ k ∗
k ∗ = { k − 1 ∣ D k 2 ϕ ∣ < ∣ D k + 1 2 ϕ ∣ k ∣ D k 2 ϕ ∣ > ∣ D k + 1 2 ϕ ∣ k ∗ = { k − 1 k ∣ D k 2 ϕ ∣ < ∣ D k + 1 2 ϕ ∣ ∣ D k 2 ϕ ∣ > ∣ D k + 1 2 ϕ ∣
第三步,依葫芦画瓢,设Q 3 Q 3
Q 3 ( x ) = c ∗ ( x − x k ∗ ) ( x − x k ∗ + 1 ) ( x − x k ∗ + 2 ) Q 3 ( x ) = c ∗ ( x − x k ∗ ) ( x − x k ∗ + 1 ) ( x − x k ∗ + 2 )
两边求导:
Q 3 ′ ( x ) = c ∗ [ 3 ( i − k ∗ ) 2 − 6 ( i − k ∗ ) + 2 ] ( Δ x ) 2 Q 3 ′ ( x ) = c ∗ [ 3 ( i − k ∗ ) 2 − 6 ( i − k ∗ ) + 2 ] ( Δ x ) 2
其中:
c ∗ = { D k ∗ + 1 / 2 3 ϕ ∣ D k ∗ + 1 / 2 3 ϕ ∣ < ∣ D k ∗ + 3 / 2 3 ϕ ∣ D k ∗ + 3 / 2 3 ϕ ∣ D k ∗ + 1 / 2 3 ϕ ∣ > ∣ D k ∗ + 3 / 2 3 ϕ ∣ c ∗ = { D k ∗ + 1 / 2 3 ϕ D k ∗ + 3 / 2 3 ϕ ∣ D k ∗ + 1 / 2 3 ϕ ∣ < ∣ D k ∗ + 3 / 2 3 ϕ ∣ ∣ D k ∗ + 1 / 2 3 ϕ ∣ > ∣ D k ∗ + 3 / 2 3 ϕ ∣
至此,Q 1 , 2 , 3 Q 1 , 2 , 3 ϕ x − ϕ x −
只有一句:开始的时候定义k = i k = i
ENO格式成于“essentially”精选,也缺陷于精选,因为“精选”就意味着丢弃。ϕ x i − ϕ x i −
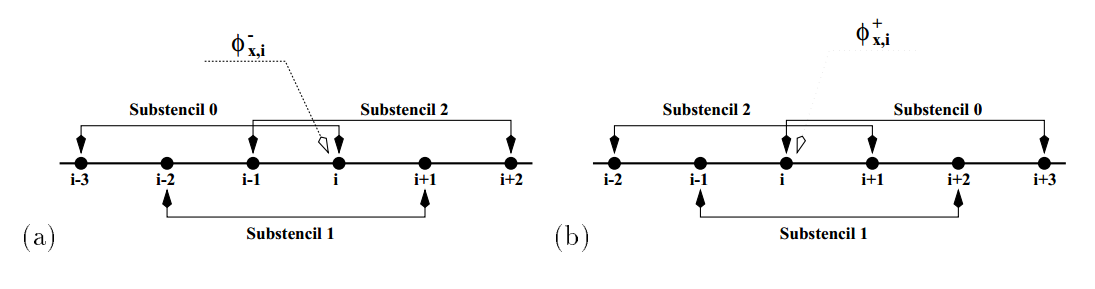
{ ϕ i − 3 , ϕ i − 2 , ϕ i − 2 , ϕ i , ϕ i + 1 , ϕ i + 2 } { ϕ i − 3 , ϕ i − 2 , ϕ i − 2 , ϕ i , ϕ i + 1 , ϕ i + 2 }
这些节点每一个都参与了计算,但是精选之后能留下来的有多少呢?
令:
v 1 = D − ϕ i − 2 v 2 = D − ϕ i − 1 v 3 = D − ϕ i v 4 = D − ϕ i + 1 v 5 = D − ϕ i + 2 v 1 = D − ϕ i − 2 v 2 = D − ϕ i − 1 v 3 = D − ϕ i v 4 = D − ϕ i + 1 v 5 = D − ϕ i + 2
ENO格式的运算实质上是一个有两个分支的流程,对其整理可以发现可能的执行结果只有下面三种:
ϕ x 1 = v 1 3 − 7 v 2 6 + 11 v 3 6 ϕ x 2 = − v 2 6 + 5 v 3 6 + v 4 3 ϕ x 3 = v 3 3 + 5 v 4 6 − v 5 6 ϕ x 1 ϕ x 2 ϕ x 3 = = = 3 v 1 − 6 7 v 2 + 6 1 1 v 3 − 6 v 2 + 6 5 v 3 + 3 v 4 3 v 3 + 6 5 v 4 − 6 v 5
两个分支下来,最后得到的只可能是这三种结果,详细的条件选择太烦,不写了,总之浪费了计算能力。
WENO的几个作者Chi-Wang Shu,Guang-Shan Jiang, Danping Peng,乍看都是中国人,不过署名学校是 University of California at Los Angeles以及Brown University。
对于证明细节也不细写,总之,在函数的光滑区间内,取ω 1 = 0.1 ω 1 = 0 . 1 ω 2 = 0.6 ω 2 = 0 . 6 ω 3 = 0.3 ω 3 = 0 . 3
ϕ x = ω 1 ϕ x 1 + ω 2 ϕ x 2 + ω 3 ϕ x 3 ϕ x = ω 1 ϕ x 1 + ω 2 ϕ x 2 + ω 3 ϕ x 3
可以得到五阶精度的导数值估计。后面又有神人证明,若在每一个ω ω O ( ( Δ x ) 2 ) O ( ( Δ x ) 2 ) ω 1 = 0.1 + O ( ( Δ x ) 2 ) ω 1 = 0 . 1 + O ( ( Δ x ) 2 ) ω 2 = 0.6 + O ( ( Δ x ) 2 ) ω 2 = 0 . 6 + O ( ( Δ x ) 2 ) ω 3 = 0.3 + O ( ( Δ x ) 2 ) ω 3 = 0 . 3 + O ( ( Δ x ) 2 )
在光滑区间内,保证ω s = ω s − o r i g i n + O ( ( Δ x ) 2 ) ω s = ω s − o r i g i n + O ( ( Δ x ) 2 )
在包含奇点的区间上,尽量消除包含奇点的计算模板的影响,也就相当于是自动选择三种ENO候选格式ϕ x i ϕ x i
显然,核心思想还是“找最光滑的”,那么首先要知道每个模板光滑程度如何。分别定义三个模板的光滑度:
S 1 = 13 12 ( v 1 − 2 v 2 + v 3 ) 2 + 1 4 ( v 1 − 4 v 2 + 3 v 3 ) S 2 = 13 12 ( v 2 − 2 v 3 + v 4 ) 2 + 1 4 ( v 2 − v 4 ) S 3 = 13 12 ( v 3 − 2 v 4 + v 5 ) 2 + 1 4 ( 3 v 3 − 4 v 4 + v 5 ) S 1 S 2 S 3 = = = 1 2 1 3 ( v 1 − 2 v 2 + v 3 ) 2 + 4 1 ( v 1 − 4 v 2 + 3 v 3 ) 1 2 1 3 ( v 2 − 2 v 3 + v 4 ) 2 + 4 1 ( v 2 − v 4 ) 1 2 1 3 ( v 3 − 2 v 4 + v 5 ) 2 + 4 1 ( 3 v 3 − 4 v 4 + v 5 )
继续定义,中间变量:
α 1 = 0.1 ( S 1 + ϵ ) 2 α 2 = 0.6 ( S 1 + ϵ ) 2 α 3 = 0.3 ( S 1 + ϵ ) 2 α 1 α 2 α 3 = = = ( S 1 + ϵ ) 2 0 . 1 ( S 1 + ϵ ) 2 0 . 6 ( S 1 + ϵ ) 2 0 . 3
其中ϵ ϵ
ϵ = 1 0 − 6 m a x { ( v 1 ) 2 , ( v 2 ) 2 , ( v 3 ) 2 , ( v 4 ) 2 , ( v 5 ) 2 } + 1 0 − 99 ϵ = 1 0 − 6 m a x { ( v 1 ) 2 , ( v 2 ) 2 , ( v 3 ) 2 , ( v 4 ) 2 , ( v 5 ) 2 } + 1 0 − 9 9
现在,可以计算得到新的ω i ω i
ω 1 = α 1 α 1 + α 2 + α 3 ω 2 = α 2 α 1 + α 2 + α 3 ω 3 = α 3 α 1 + α 2 + α 3 ω 1 ω 2 ω 3 = = = α 1 + α 2 + α 3 α 1 α 1 + α 2 + α 3 α 2 α 1 + α 2 + α 3 α 3
用这个加权平均即可。WENO格式除初始化(选择 ϕ x + ϕ x + ϕ x − ϕ x − ϕ x − ϕ x − ϕ x − ϕ x − v i v i
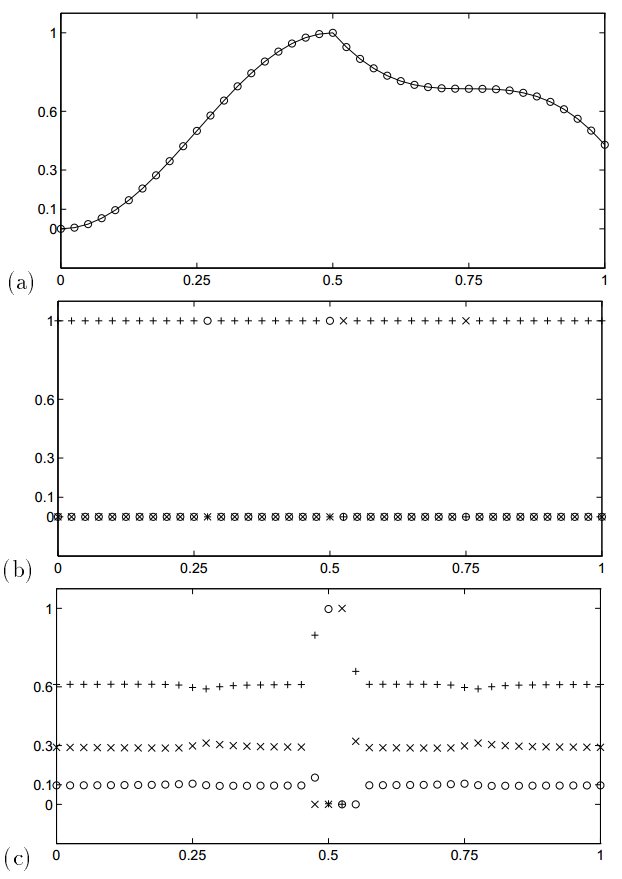
如图,(a)图为函数图像,(b)图为ENO的“权重取值”,只有0和1,因为ENO格式只取一个,(c)图为WENO算法下的权重。后面两图中,○+×分别代表123项的权重。可以看出,在多数情况下,WENO的权重很接近0.1、0.6、0.3,但是在接近奇点处会自动调整为更合适的值,保证数值计算的稳定性。